Der Thaleskreis

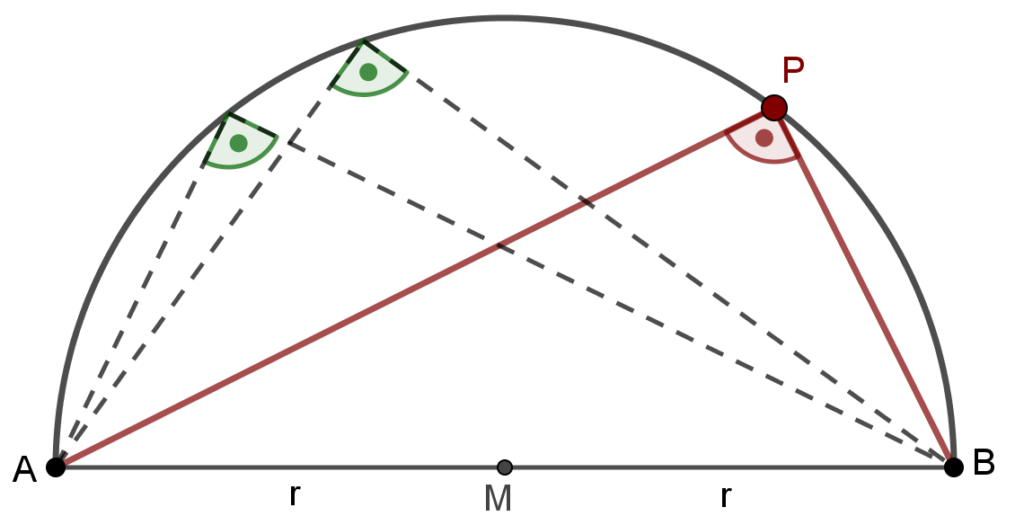
Gegeben ist ein Halbkreis mit dem Durchmesser $AB$ , dem Mittelpunkt $M$ und dem Radius $r$ . Wählt man einen beliebigen Punkt $P$ auf dem Kreisbogen aus und verbindet diesen Punkt mit den Endpunkten $A$ und $B$ des Durchmessers, dann ist der Winkel $\mathbf{\angle APB}$ im Punkt $\mathbf{P}$ immer ein rechter Winkel. Der erste Beweis dieser Aussage wird dem griechischen Mathematiker und Philosophen Thales von Milet zugeschrieben. Der in diesem Beitrag beschriebene Beweis basiert auf dem von Thales von Milet geführten Beweis. Ein deratiger Halbkreis wird als Thaleskreis bezeichnet.

Beweis:

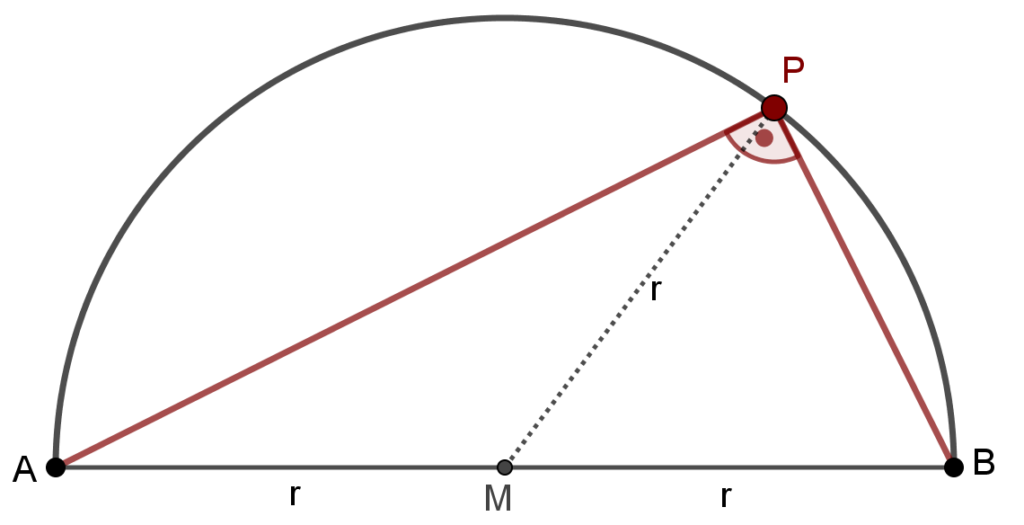
Wir wählen einen beliebigen Punkt $P$ auf dem Halbkreisbogen aus. Die Punkte $A, B$ und $P$ bilden ein Dreieck von dem wir nun zeigen wollen, dass der Winkel $\mathbf{\angle APB}$ im Punkt $\mathbf{P}$ ein rechter Winkel ist.

Indem wir den Radius vom Mittelpunkt zum Punkt $P$ einzeichnen, teilen wir das Dreieck $ABP$ in zwei Dreiecke $AMP$ und $MBP$ (siehe obenstehende Abbildung).

Die beiden so erhaltenen Dreieck sind gleichschenkelig, weil die Seiten $AM, MP$ und $MB$ jeweils die Länge $r$ haben.

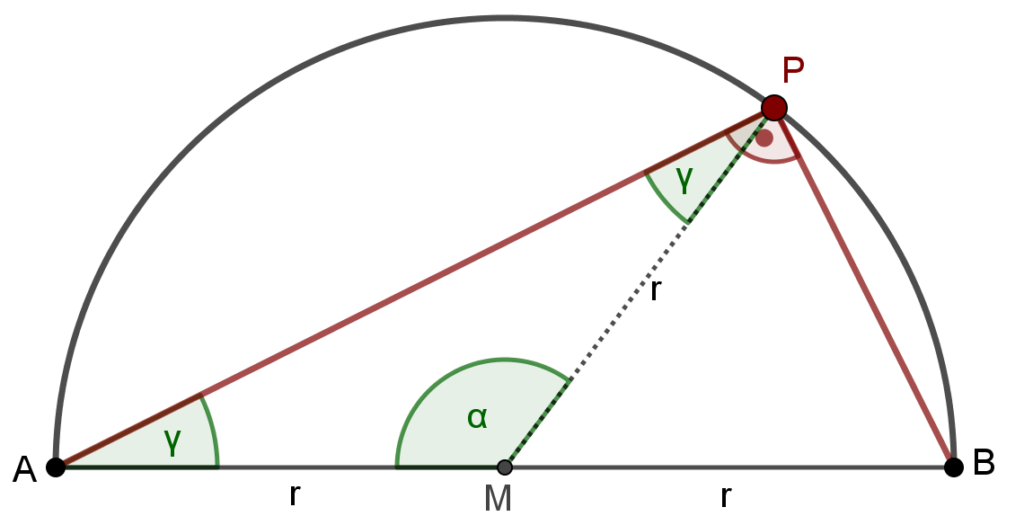Im Dreieck $APB$ bezeichnen wir den Winkel an der Spitze $M$ mit $\alpha$ und die Basiswinkel mit $\gamma$ , dann gilt:

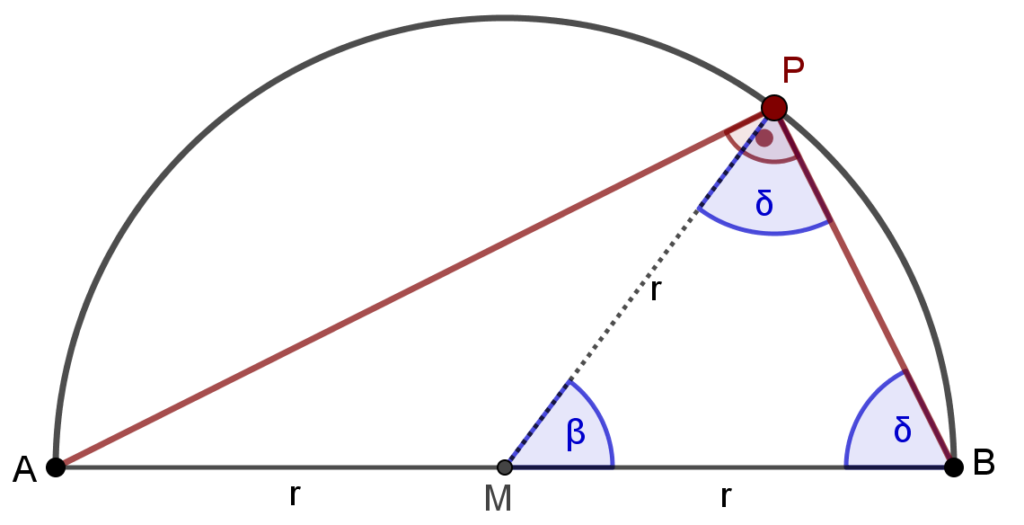\alpha + 2 \cdot \gamma = 180°~\Rightarrow~\gamma = \frac{180°-\alpha}{2}

Im Dreieck $MBP$ führen wir eine analoge Beschriftung ein. Den Winkel an der Spitze $M$ bezeichnen wir mit $\beta$ und die beiden Basiswinkel werden mit $\delta$ bezeichnet.

Es gilt dann:

\beta + 2 \cdot \delta = 180°~\Rightarrow~\delta = \frac{180°-\beta}{2}

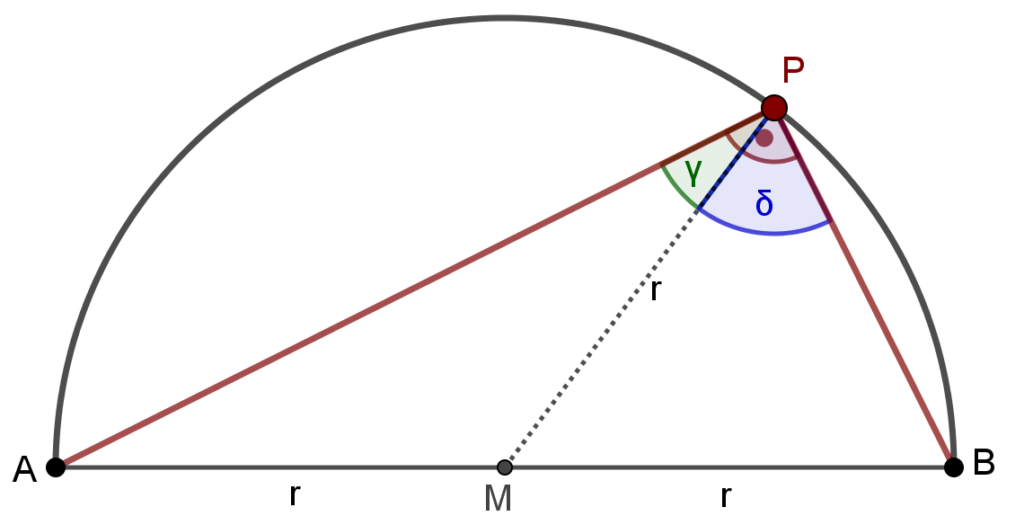Der Winkel $\angle APB$ im Punkt $P$ setzt sich zusammen aus den beiden Winkeln $\gamma$ und $\delta$ :

\gamma + \delta = \frac{180° - \alpha}{2} + \frac{180° - \beta}{2} = \newline

~~~~~~~~~~= 90° - \frac{\alpha}{2} + 90° - \frac{\beta}{2} = \newline

~~~~~~~~~~= 180° - \frac{\alpha + \beta}{2} \newline

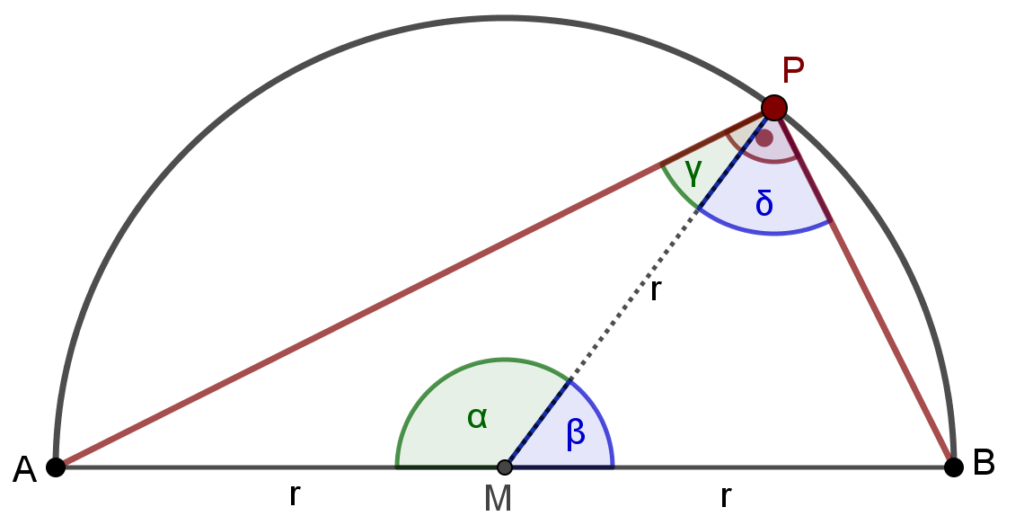
Die Summe der Winkel $\alpha$ und $\beta$ ergibt einen Winkel von $180°$ . Damit gilt:

\mathbf{ \gamma + \delta }= 180° - \frac{\overbrace{\alpha + \beta}^{=180°}}{2} = \mathbf{90°}\newline

Konstruktion einer Tangente aus einem Punkt an den Kreis

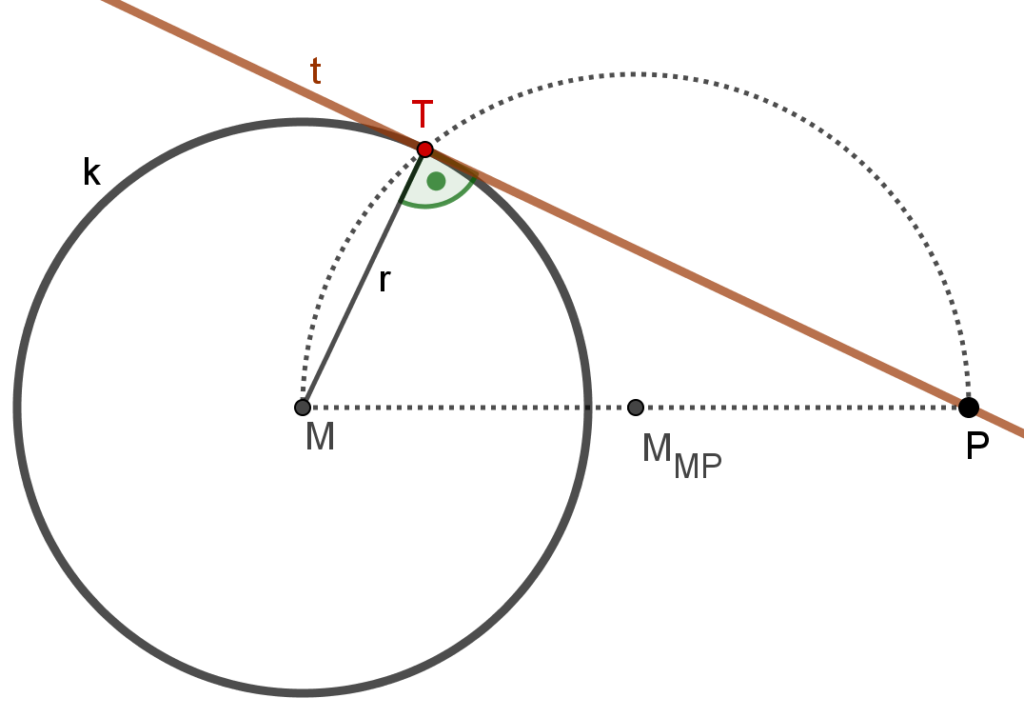Eine Anwendung für den Thaleskreis ist die Konstruktion einer Tangente aus einem Punkt $P$ an einen Kreis $k$ . Dabei nutzt man den Umstand, dass die Verbindungsstrecke vom Mittelpunkt $M$ des Kreises zum Berührungspunkt $T$ normal auf die Tangente steht. Zur Konstruktion der Tangente geht man wie folgt vor:

Zeichne über der Strecke $MP$ einen Halbkreis.
Markiere den Schnittpunkt des Halbkreises mit dem Kreis $k$ und beschrifte ihn mit $T$ .
Zeichne die Tangente an den Kreis als Gerade durch die Punkte $P$ und $T$ .