Die Satzgruppe des Pythagoras

Die Satzgruppe des Pythagoras umfasst drei Aussagen über rechtwinkelige Dreiecke:

• Hauptsatz: a^2 + b^2 = c^2
• Höhensatz: h^2 = q \cdot p
• Kathetensätze: a^2 = p \cdot c,~~~b^2 = q \cdot c

Wenn man vom Satz des Pythagoras spricht, ist meist nur der Hauptsatz gemeint.

Der Hauptsatz

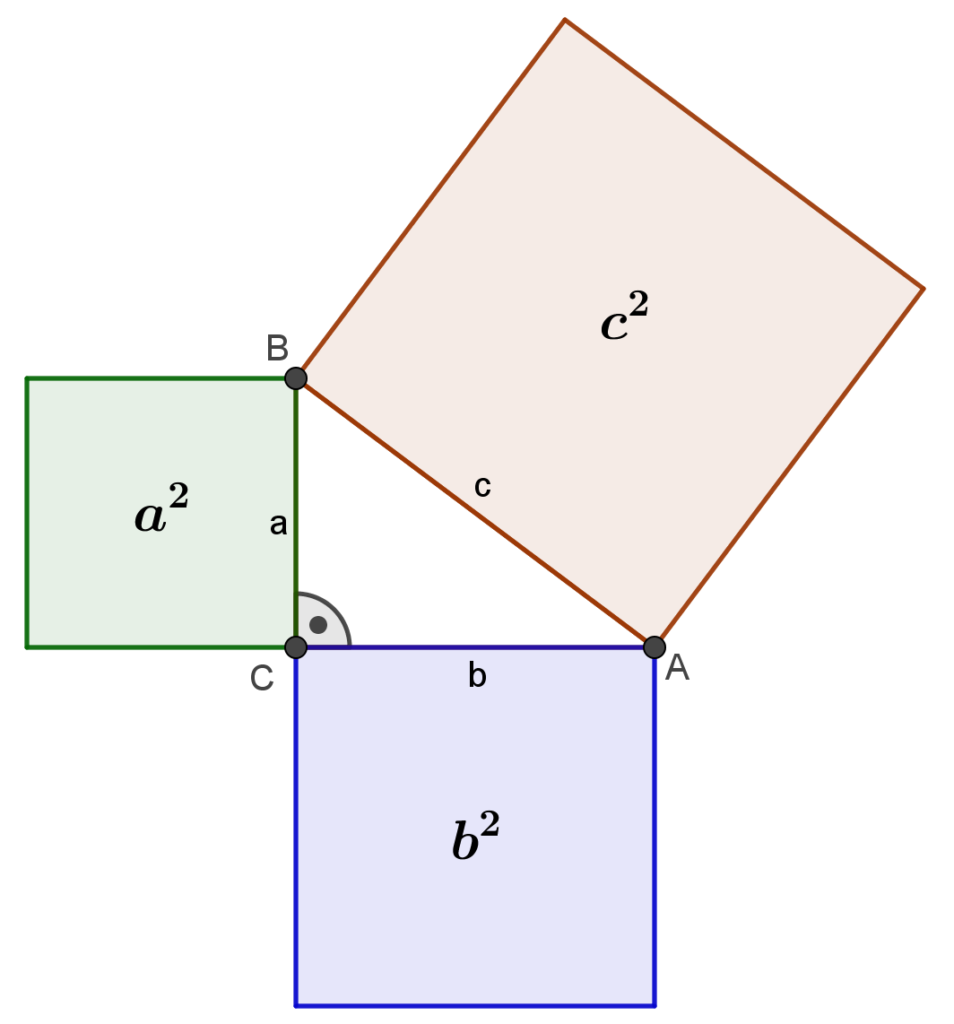Aus der Satzgruppe des Pythagoras ist der Hauptsatz einer der fundamentalen Sätze der euklidischen Geometrie. Er besagt, dass in allen rechtwinkeligen Dreiecken die Summe der Kathetenquadrate gleich dem Flächeninhalt des Hypotenusenquadrat ist.

\mathbf{\boxed{a^2 + b^2 = c^2}}

Dieser Satz ist nach Pythagoras von Samos benannt, weil er der als Erster einen Beweis für diesen Satz gefunden haben soll. Die Aussage dieses Satzes war zwar schon lange vor Pythagoras in Babylonien und Indien bekannt, es gibt aber keinen Nachweis dafür, dass man in diesen Ländern auch einen Beweis hatte.

Beweis:

Für den Beweis gehen wir von einem Quadrat mit den Seitenlängen a + b aus (braun eingefärbt), dem ein Quadrat mit der Seitenlänge c (grün eingefärbt) eingeschrieben wird.

Der Flächeninhalt des großen Quadrats errechnet sich aus:

\left( a + b \right)^2 = a^2 + 2ab + b^2

Der Flächeninhalt des kleinen Quadrats ist c^2, Er kann aber auch aus dem Flächeninhalt des großen Quadrats berechnet werden.

Dazu subtrahiert man vom Flächeninhalt des große Quadrats die Flächeninhalte der braun eingefärbten Dreiecke. All diese Dreiecke sind deckungsgleich und ihr Flächeninhalt ergibt sich aus A = \frac{a \cdot b}{2}. Für den Flächeninhalt des grünen Quadrats erhält man damit:

c^2 = \left( a + b \right)^2 - 4 \cdot \frac{a \cdot b}{2} = \newline ~~~~= a^2 + 2ab + b^2  - 2ab = \newline ~~~~= a^2 + b^2

Erweiterung des Satzes von Pythagoras

Der Satz von Pythagoras gilt auch dann, wenn man an den Seiten des Dreiecks anstelle von Quadraten andere geometrische Figuren verwendet.

Satz des Pythagoras für Halbkreise

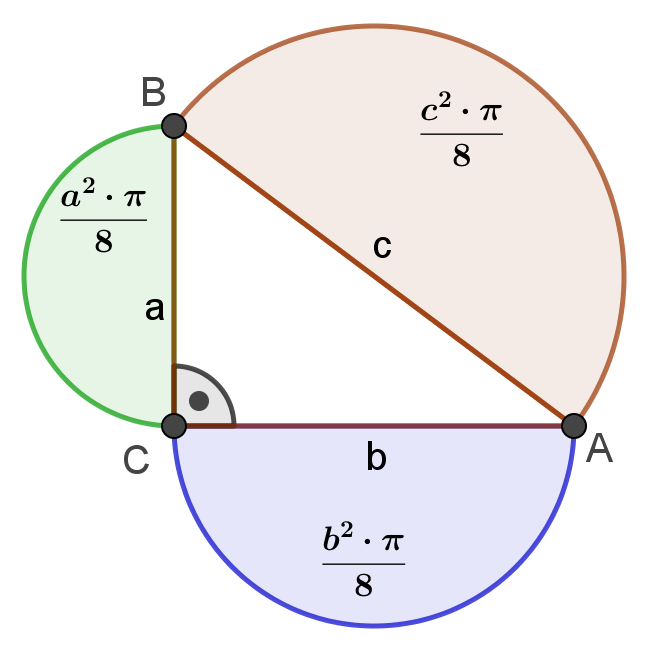Anstelle der Quadrate zeichnen wir an jeder Seite des Dreiecks einen Halbkreis (siehe nebenstehende Abbildung).

Für den Flächeninhalt des Halbkreises an der Seite a des Dreiecks gilt: der Radius entspricht der halben Seitenlänge,  d.h. r_a = \frac{a}{2}. Der Flächeninhalt ergibt sich dann aus:

A_a = \frac{1}{2}\cdot r_a^2\cdot \pi = \frac{1}{2} \left( \frac{a}{2}\right)^2\cdot\pi = \frac{a^2\cdot\pi}{8}

Analog erhält man für die Flächeninhalte der beiden Seiten b und c:

A_b = \frac{b^2\cdot\pi}{8} \newline A_c = \frac{c^2\cdot\pi}{8}

Addieren wir die Flächeninhalte der beiden Halbkreise an den Katheten, sollte sich nach dem Satz des Pythagoras der Flächeninhalt des Halbkreises an der Hypotenus ergeben:

A_a + A_b = \frac{a^2\cdot\pi}{8} + \frac{b^2\cdot\pi}{8} = \frac{c^2\cdot\pi}{8} = A_c \newline

Durch Umformen der Gleichung erhält man:

\frac{a^2\cdot\pi}{8} + \frac{b^2\cdot\pi}{8} = \frac{c^2\cdot\pi}{8}~~~\vert~\cdot 8 \newline a^2\cdot\pi + b^2\cdot\pi = c^2\cdot\pi~~~\vert~\div \pi\newline \mathbf{a^2 + b^2 = c^2}

Satz des Pythagoras für gleichseitige Dreiecke

Anstelle der Quadrate zeichnen wir an jeder Seite des Dreiecks ein gleichseitiges Dreieck (siehe nebenstehende Abbildung).

Für den Flächeninahl des gleichseitigen Dreiecks an der Seite a des Dreiecks gilt:

A_a = \frac{a^2\cdot\sqrt{3}}{4}

Entsprechendes gilt für die Flächeninhalte der gleichseitigen Dreiecke an den Seiten b und c:

A_b = \frac{b^2\cdot\sqrt{3}}{4},~~~A_c= \frac{c^2\cdot\sqrt{3}}{4}

Addieren wir die Flächeninhalte der beiden gleichseitigen Dreiecke an den Katheten, sollte sich nach dem Satz des Pythagoras der Flächeninhalt des gleichseitigen Dreiecks an der Hypotenuse ergeben:

A_a + A_b = \frac{a^2\cdot\sqrt{3}}{4} + \frac{b^2\cdot\sqrt{3}}{4} = \frac{c^2\cdot\sqrt{3}}{4} = A_c \newline

Durch Umformen der Gleichung erhält man:

\frac{a^2\cdot\sqrt{3}}{4} + \frac{b^2\cdot\sqrt{3}}{4} = \frac{c^2\cdot\sqrt{3}}{4} ~~~~~\vert~\cdot  4\newline a^2\cdot\sqrt{3} + b^2\cdot\sqrt{3} = c^2\cdot\sqrt{3} ~~~~~\vert~\div  \sqrt{3}\newline \mathbf{a^2 + b^2 = c^2}

Der Höhensatz

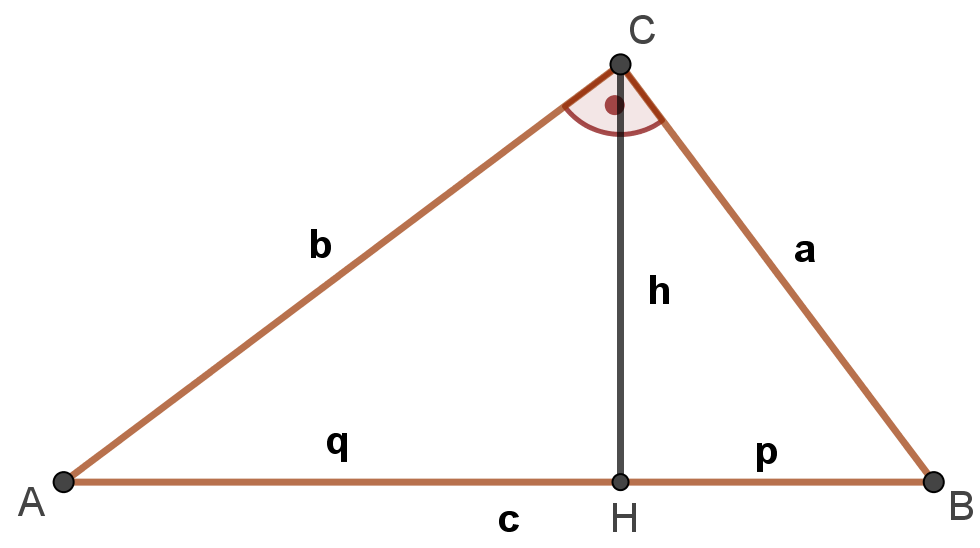Durch Einzeichnen der Höhe h auf die Hypothenuse c wird diese in die beiden Abschnitte q und p geteilt. Der Höhensatz besagt dann, dass in jedem rechtwinkeligen Dreieck der Flächeninhalt des Quadrats über der Höhe h gleich ist dem Flächeninhalt eines Rechtecks mit den Seitenlängen q und p, d.h.

\boxed{\mathbf{h^2 = q \cdot p}}

Beweis:

Weil die Höhe h auf die Grundlinie c normal steht, sind die Dreiecke \Delta AHC und \Delta HBC jeweils rechtwinkelige Dreiecke. Wegen des Hauptsatzes gilt für das Dreieck \Delta AHC

q^2 + h^2 = b^2

und für das Dreieck \Delta HBC gilt:

p^2 + h^2 = a^2

Die Addition der beiden Gleichungen ergibt:

q^2 + p^2 + 2h^2 = \underbrace{a^2 + b^2}_{=c^2}~~~\Rightarrow~~~q^2 + p^2 + 2h^2 = c^2

Die Seite c setzt sich aus den beiden Abschnitten q und p zusammen, d.h. es gilt:

c = q + p~~~~~\Rightarrow~~~~~c^2 = \left( q + p \right)^2 = q^2 + 2qp + p^2

Setzen wir dieses Ergebnis oben für c^2  ein, erhalten wir:

q^2 + p^2 + 2h^2 = c^2 \\ q^2 + p^2 + 2h^2 = q^2 + 2qp + p^2~~~\vert~-q^2-p^2 \\ 2h^2 = 2qp~~~\vert~\div~-2 \\ \mathbf{h^2 = qp}

Die Kathetensätze

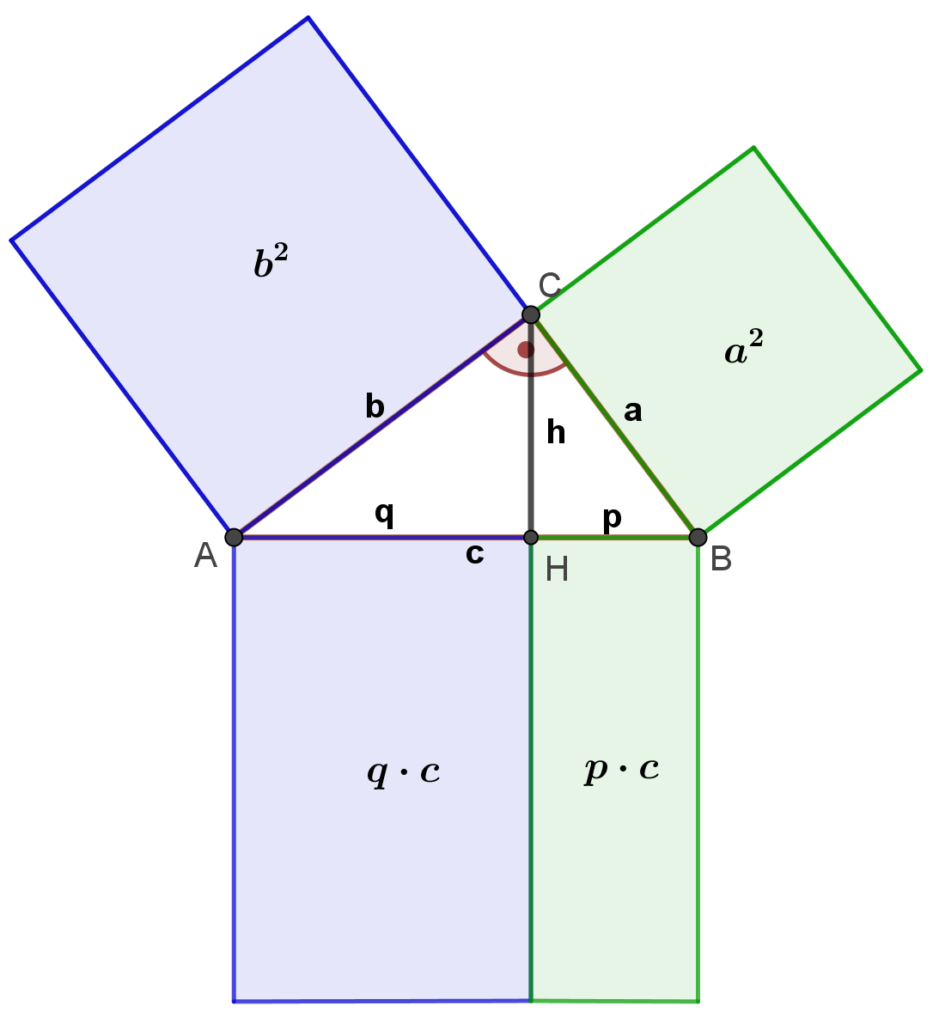Die Kathetensätze besagen, dass in jedem rechtwinkeligen Dreieck der Flächeninhalt

• des Quadrats über der Kathete a gleich ist dem Flächeninhalt eines Rechtecks mit den Seitenlängen p und c (in nebenstehender Abbildung grün eingefärbt): \boxed{\mathbf{p\cdot c = a^2} }
• des Quadrats über der Kathete b gleich ist dem Flächeninhalt eines Rechtecks mit den Seitenlängen q und c (in nebenstehender Abbildung blau eingefärbt): \boxed{\mathbf{q\cdot c = b^2} }

Beweis:

Für den Beweis der Gültigkeit der Kathetensätze verwenden wir den Höhensatz:

\mathbf{p\cdot c} = p \cdot \overbrace{\left( q+p\right)}^{=c} = p^2 + \overbrace{qp}^{=h^2} = \overbrace{p^2 + h^2}^{=a^2} = \mathbf{a^2} \\ \mathbf{q\cdot c} = q \cdot \overbrace{\left( q+p\right)}^{=c} = q^2 + \overbrace{qp}^{=h^2} = \overbrace{q^2 + h^2}^{=b^2} = \mathbf{b^2}

Pythagoreische Tripel

In der Zahlentheorie werden drei natürliche Zahlen x, y, z \in \mathbb{N} ein pythagoreisches Tripel genannt, wenn sie als Seiten eines rechtwinkeligen Dreiecks vorkommen können, d.h. wenn sie den Hauptsatz des Pythagoras erfüllen, wenn also gilt: x^2 + y^2 = z^2

Beispiele pythagoreischer Tripel:

\begin{array}{lclcl} \left( 3, 4, 5\right)& \Rightarrow &  3^2 + 4^2 & = & 5^2 \\ \left( 5, 12, 13 \right)& \Rightarrow & 5^2 + 12^2 & = & 13^2 \\ \left( 8, 15, 17 \right)& \Rightarrow & 8^2 + 15^2 & = & 17^2\end{array} 

Erzeugung pythagoreischer Tripel

Zur Erzeugung eines pythagoreischen Tripels wählt man zwei beliebige natürliche Zahlen u und v mit u \gt v. Zur Berechnung der Zahlen x, y und z verwendet man die folgenden Gleichungen:

\begin{array}{lcl}x &=& u^2 - v^2 \\ y &=& 2\cdot u\cdot v \\ z &=& u^2 + v^2\end{array}

Arbelos

Ein Arbelos ist eine spezielle, von drei Halbkreisen begrenzte geometrische Figur. Die Bezeichnung Arbelos kommt aus dem Griechischen und bedeutet Schustermessser (siehe nebenstehende Abbildung). Die Eigenschaften dieser Figur sollen vom griechischen Mathematiker Archimedes untersucht und in seinem Buch der Lemmata beschrieben worden sein.

Eine wesentliche Eigenschaft eines Arbelos ist, dass sein Flächeninhalt (in nebenstehender Abbildung grün markiert) gleich groß ist wie der Flächeninhalt des Kreises k, dessen Durchmesser der Höhe h_c entspricht.

Beweis

Nach dem Satz des Thales ist das Dreieck ABC ein rechtwinkeliges Dreieck mit dem rechten Winkel im Punkt C. Die Höhe h_c teilt die Hypotenuse in die beiden Hypotenusenabschnitte q und p.

Berechnung des Flächeninhalts des Kreises \mathbf{k}:

Der Radius des Kreises k entspricht der halben Höhe auf die Seite AB:

r = \frac{h_c}{2}~\Rightarrow~A = \frac{h_c^2 \cdot \pi}{4}

Berechnung des Flächeninhalts des Arbelos:

Der Flächeninhalt des Arbelos ergibt aus der Fläche A_r des Halbkreises mit dem Radius r  = \frac{\overline{AB}}{2}. Von dieser Fläche müssen die Flächen A_1 und A_2 zweier Halbkreise mit den Radien r_1 = \frac{q}{2} und r_2 = \frac{p}{2} subtrahiert werden. Die Flächeninhalte dieser Halbkreise sind:

\begin{array}{lcl} A_r &=& \frac{r^2\cdot \pi }{2}\\A_1 &=& \frac{1}{2}\cdot\frac{q^2\cdot \pi}{4} \\ A_2 &=& \frac{1}{2}\cdot\frac{q^2\cdot \pi}{4} \end{array}\newline

Für den Flächeninhalt des Kreises k erhält man damit:

A = A_r - A_1 - A_2 = \frac{r^2 \cdot \pi}{2} - \frac{q^2\cdot\pi}{8} - \frac{p^2\cdot\pi}{8} = \pi \cdot \left( \frac{r^2}{2} - \frac{q^2 + p^2}{8}\right)

Weil wir weiter oben für A = \frac{h_c^2 \cdot \pi}{4} erhalten haben, können wir schreiben:

\begin{array}{lclcl} \frac{h_c^2 \cdot \pi}{4} &=& \pi \cdot \left( \frac{r^2}{2} - \frac{q^2 + p^2}{8}\right) & \mid & : \pi \cdot 8  \\ 2 \cdot h_c &=& 4\cdot r^2 - q^2 - p^2 &  & \end{array}

Wegen des Höhensatzes gilt: h_c^2 = q \cdot p. Damit können wir obige Gleichung schreiben als:

\begin{array}{lclcl} 2 \cdot h_c &=& 4\cdot r^2 - q^2 - p^2 &  & \\ 2 \cdot q\cdot p &=& 4\cdot r^2 - q^2 - p^2 & \mid &+ q^2 + p^2 \\ \underbrace{q^2 + 2 \cdot q\cdot p + p^2}_{=\left( q + p \right)^2} &=& 4\cdot r^2  &  & \\ \\ \left( q+p \right)^2 &=& 4\cdot r^2  &  & \end{array}

 

Die Summe q + p entspricht dem Durchmesser \overline{AB} des Halbkreises von A nach B, es gilt daher: \overline{AB} = p + q = 2 \cdot r~\Rightarrow~\left( q + p \right)^2 = \left( 2r \right)^2 = 4r^2.

Die Zwölfkotenschnur

Die Zwölfknotenschnur wurde von den alten Ägyptern zur Messung von rechten Winkeln verwendet. Dabei handelt es sich um eine geschlossene Schnur (Ring), die in 12 gleich große Teile unterteilt wurde. Damit ist es möglich, dieses Seil als rechtwinkeliges Dreieck mit den Seitenlängen a = 3,~~b = 4,~~c = 5 aufzuspannen. Der von den beiden kürzeren Seiten eingeschlossene Winkel wird automatisch zu einem rechten Winkel.

Die Zwölfknotenschnur wurde unter der Bezeichnung Maurerwinkel lange auf Baustellen verwendet, um rechte Winkel einzumessen.