Als Quadratzahlen bezeichnet man eine Zahl a, die durch die Multiplikation einer ganzen Zahl n mit sich selbst entsteht:
a = n \cdot n = n^2 \newlineDie ersten Quadratzahlen sind 0, 1, 4, 9, 16, 25, 36, 49, 64, 81, 100, ... \newline
Die 0 erfüllt zwar die Bedinung einer Quadratzahl, wird aber von einigen Autoren nicht als Quadratzahl betrachtet.
 Die Bezeichung Quadratzahl leitet sich davon ab, dass die Anzahl der Steine zum Legen eines Quadrates immer eine Quadratzahl ist. Für das Legen eines Quadrates mit der Seitenlänge a = 1 benötigt man a^2 = 1 Steine. Für ein Quadrat mit der Seitenlänge a = 2 benötigt man a^2 = 4 Steine, das sind um 3 Steine mehr.
Die Bezeichung Quadratzahl leitet sich davon ab, dass die Anzahl der Steine zum Legen eines Quadrates immer eine Quadratzahl ist. Für das Legen eines Quadrates mit der Seitenlänge a = 1 benötigt man a^2 = 1 Steine. Für ein Quadrat mit der Seitenlänge a = 2 benötigt man a^2 = 4 Steine, das sind um 3 Steine mehr.
Für ein Quadrat mit der Seitenlänge a = 3 benötigt man a^2 = 9 Steine, also um 5 Steine mehr, als ein Quadrat mit der Seitenlänge a = 2.
Für ein Quadrat mit der Seitenlänge a = 4 benötigt man a^2 = 16 Steine, also um 7 Steine mehr, als ein Quadrat mit der Seitenlänge a = 3.
Formel zum Generieren von Quadratzahlen
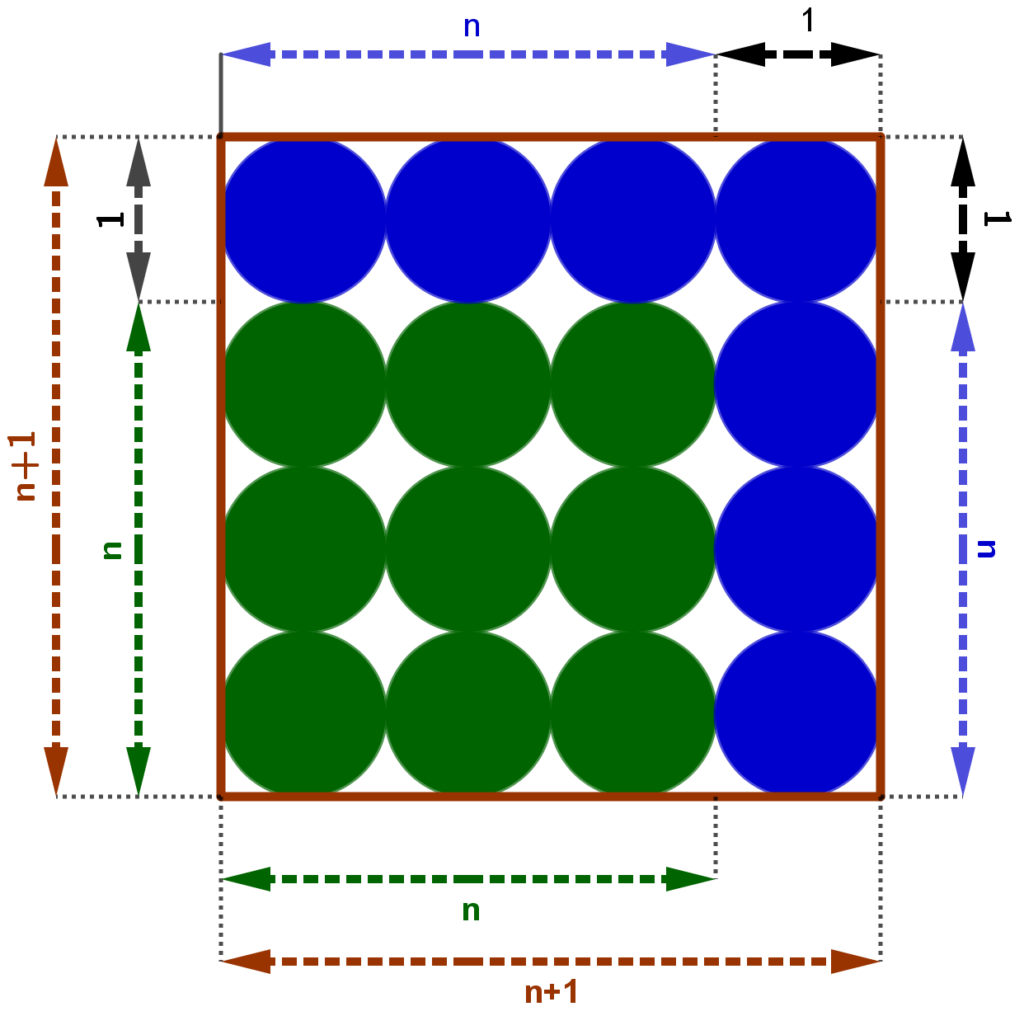
Aus der obigen Abbildung lässt sich eine Formel zur Berechnung der zu einer Quadratzahl q_1 = n^2 benachbarten Quadratzahl q_2 = \left( n + 1 \right)^2 herleiten.
 Für ein Quadrat mit der Seitenlänge n + 1 benötigt man q_2 = \left( n + 1 \right)^2 Steine. Dieser Ausdruck ist eine binomische Formel und ergibt ausgerechnet:
Für ein Quadrat mit der Seitenlänge n + 1 benötigt man q_2 = \left( n + 1 \right)^2 Steine. Dieser Ausdruck ist eine binomische Formel und ergibt ausgerechnet:
Für ein Quadrat mit der Seitenlänge n +1 benötigen wir zu den q_1 = n^2 Steinen für das Quadrat mit der Seitenlänge n (grün eingefärbt) zusätzlich noch 2n + 1 Steine (blau eingefärbt).
Die Differenz zwischen zwei Quadratzahlen ergibt also:
\boxed{\mathbf{q_2 - q_1 = 2n + 1}}\newlineFür jede beliebige natürliche Zahl n ist 2n + 1 eine ungerade Zahl \Rightarrow die Differenz zweier benachbarter Quadratzahlen ist immer eine ungerade Zahl.
Eigenschaften
Zusammenhang zwischen Quadratzahlen und natürlichen Zahlen
Jede Quadratzahl q = n^2 ist die zweifache Summe der ersten n - 1 natürlichen Zahlen plus der Basis n.
Beweis:
Die Summe der ersten natürlichen Zahlen n - 1 plus n ergibt:
1 + 2 + 3 + ... + \left( n - 1 \right) = 2 \cdot \frac{n \cdot \left( n - 1\right)}{2} = n \cdot \left( n - 1\right) = n^2 - n
Addiert man zu diesem Ergebnis die Ausgangszahl n ergibt sich die Quadratzahl q = n^2.
Gerade Quadratzahlen
Eine Quadratzahl ist genau dann eine gerade Zahl, wenn ihre Basis n eine gerade Zahl ist.
Beweis:
Jede gerade Zahl n kann durch Multiplikation einer natürlichen Zahl i mit 2 erzeugt werden: n = 2\cdot i ergibt für i = 0, 1, 2, 3, ... die geraden Zahlen 0, 2, 4, 6, ...
Das Quadrat einer geraden Zahl ergibt dann:
n^2 = \left( 2i \right)^2 = 4 \cdot i^2.
Die Zahl n^2 ist also ein Vielfaches von 4. Weil jede Zahl, die ein Vielfaches von 4 ist, auch ein Vielfaches von 2 ist, muss diese Zahl eine gerade Zahl sein.
Nähungswert für \pi berechnen
Die Summe der Kehrwerte aller Quadratzahlen ergibt \frac{\pi^2}{6}
\Sigma_\infty = \sum\limits_{i = 1}^{\infty}\frac{1}{n^2} = \frac{1}{1^2} + \frac{1}{2^2} + \frac{1}{3^2} + \frac{1}{4^2} + \frac{1}{5^2} + ... = \frac{\pi^2}{6}
Diese Beziehung kann verwendet werden, um die Zahl \pi näherungsweise zu berechnen. Durch Umformung der Gleichung erhält man:
\Sigma_\infty = \frac{\pi^2}{6}~~~~~\Rightarrow~~~~~\boxed{\mathbf{\pi = \sqrt{6\cdot \Sigma_\infty}}}
Die folgende Tabelle zeigt die Ergebnisse für die näherungsweise Berechnung von \pi für die ersten 200 Quadratzahlen.
| i | Summe | Annäherung von \pi |
| 1 | \Sigma_1 = \frac{1}{1^2} = 1 | 2,449489743 |
| 2 | \Sigma_2= \Sigma_1 + \frac{1}{2^2} = 1,25 | 2,738612788 |
| 3 | \Sigma_3 = \Sigma_2 + \frac{1}{3^2} = 1,3611111 | 2,8577380338 |
| 4 | \Sigma_4 = \Sigma_3 + \frac{1}{4^2} = 1,423611111 | 2,922612986 |
| 5 | \Sigma_5 = \Sigma_4 + \frac{1}{5^2} = 1,463611111 | 2,923387701 |
| 6 | \Sigma_6 = \Sigma_5 + \frac{1}{6^2} = 1,491388889 | 2,991376495 |
| : | : | : |
| 200 | \Sigma_{200} = \Sigma_{199} + \frac{1}{200^2} = 1,639946546 | 3,136826306 |
Die Annäherung an den Wert von \pi erfolgt ziemlich langsam, daher hat diese Methode zur Berechnung der Kreiszahl \pi keine praktische Bedeutung. Weitere Methoden zur Berechnung der Kreiszahl \pi werden im Beitrag „Die Kreiszahl“ beschrieben.