Addition und Subtraktion rationaler Zahlen
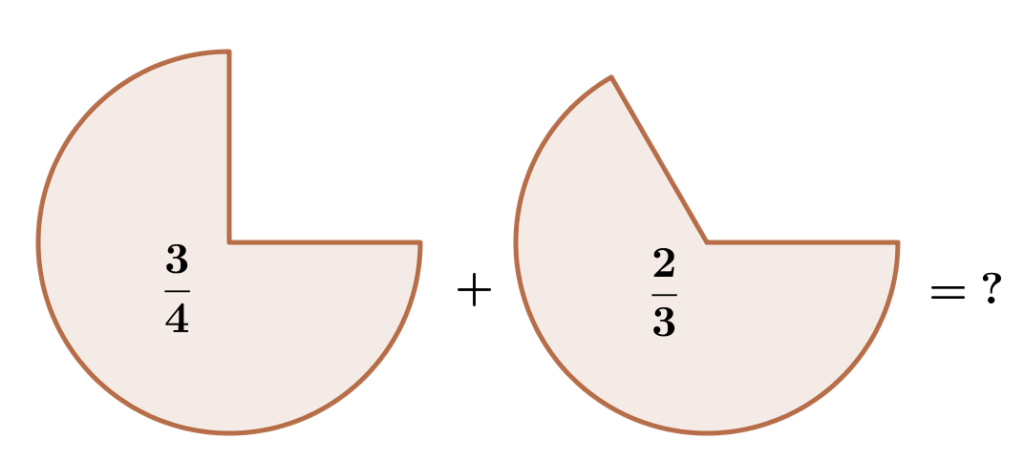Angenommen, wir haben \frac{3}{4} einer Pizza und \frac{2}{3} einer weiteren Pizza. Wie viele Pizzen haben wir dann insgesamt?
Zur Berechnung der Summe zerschneiden wir jede der beiden Pizzen in Teilstücke gleicher Größe. Das Zerschneiden soll so erfolgen, dass alle Teilstücke beider Pizzen gleich groß sind. Wie groß müssen dann die Teilstücke sein?
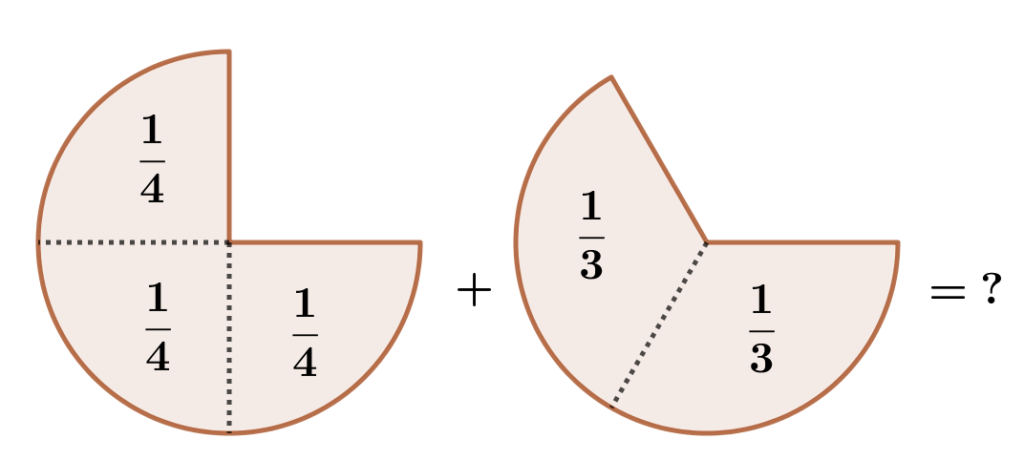Wenn wir \frac{3}{4} einer Pizza haben, dann kann man sich diese Pizza aus 3 mal einem Viertel einer ganzen Pizza zusammengesetzt denken. Entsprechend kann man sich die zweite Pizza aus 2 mal einem Drittel einer ganzen Pizza zusammengesetzt denken.
Wenn wir nun jedes Viertel der ersten Pizza halbieren, erhalten wir Stücke, die jeweils \frac{1}{4} \div 2 = \frac{1}{4 \cdot 2} = \mathbf{\frac{1}{8}} einer ganzen Pizza ausmachen. Teilen wir ein Viertel in drei Teile, hat jeder Teil \frac{1}{4} \div 3 = \frac{1}{4 \cdot 3} = \mathbf{\frac{1}{12}} der Größe einer ganzen Pizza. Teilen wir ein Viertel in n Teile, hat jeder Teil \mathbf{\frac{1}{4 \cdot n}} der Größe einer ganzen Pizza.
Für die zweite Pizza führen wir eine analoge Überlegung durch. Wenn wir jedes Drittel der zweiten Pizza halbieren, erhalten wir Stücke, die jeweils \frac{1}{6} einer ganzen Pizza ausmachen. Teilen wir ein Drittel in drei Teile, hat jeder Teil \frac{1}{9} der Größe einer ganzen Pizza. Teilen wir ein Drittel in n Teile, hat jeder Teil \mathbf{\frac{1}{3 \cdot n}} der Größe einer ganzen Pizza.
Wie wir oben gesehen haben, sind die Nenner der beim Zerschneiden entstandenen Pizzateile im Falle der ersten Pizza Vielfache von 4 und im Falle der zweiten Pizza Vielfach von 3. Die Teile der beiden Pizzen sind dann gleich groß, wenn die Nenner der Bruchteile beider Pizzen ein gemeinsames Vielfaches von 4 und 3 sind.
Die folgende Tabelle zeigt Vielfache von \color{blue}4 und \color{orange}3.
\begin{array}{|c|c|c|c|c|c|}\hline &1&2&\mathbf{\color{blue}3}&\mathbf{\color{orange}4}&... \\ \hline \textrm{Vielfache von }\mathbf{\color{blue}4}&4&8&\mathbf{\color{brown}12}&16&...\\ \hline \textrm{Vielfache von }\mathbf{\color{orange}3}&3&6&9&\mathbf{\color{brown}12}&... \\ \hline \end{array}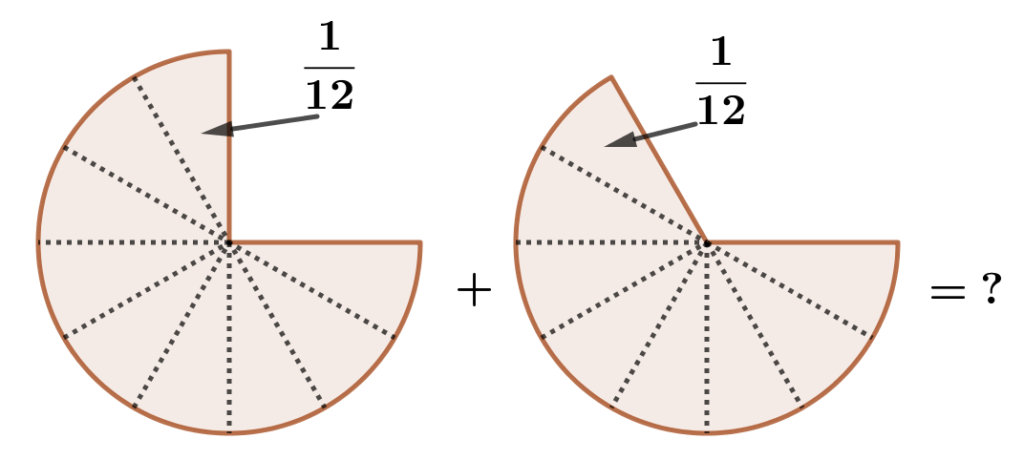
Das erste gemeinsame Vielfache von 4 und 3 ist \mathbf{\color{brown}12}. Die beiden Pizzen müssen so zerschnitten werden, dass die entstehenden Stücke \mathbf{\color{brown}\frac{1}{12}} der Größe einer ganzen Pizza haben.
Um die geforderte Größe der Pizzastücke zu erhalten, Teilen wir jedes \textcolor{blue}{\textbf{Viertel}} der ersten Pizza in \mathbf{\color{blue}3} Teile und jedes \textcolor{orange}{\textbf{Drittel}} der zweiten Pizza in \color{orange}{\mathbf{4}} Teile, dann haben alle Pizzaschnitten der beiden Pizzen die selbe Größe. Sie haben jeweils \color{brown}\mathbf{\frac{1}{12}} der Größe einer ganzen Pizza. Bei der ersten Pizza erhalten wir 9 solche Schnitten, bei der zweiten Pizza sind es 8 Teile.
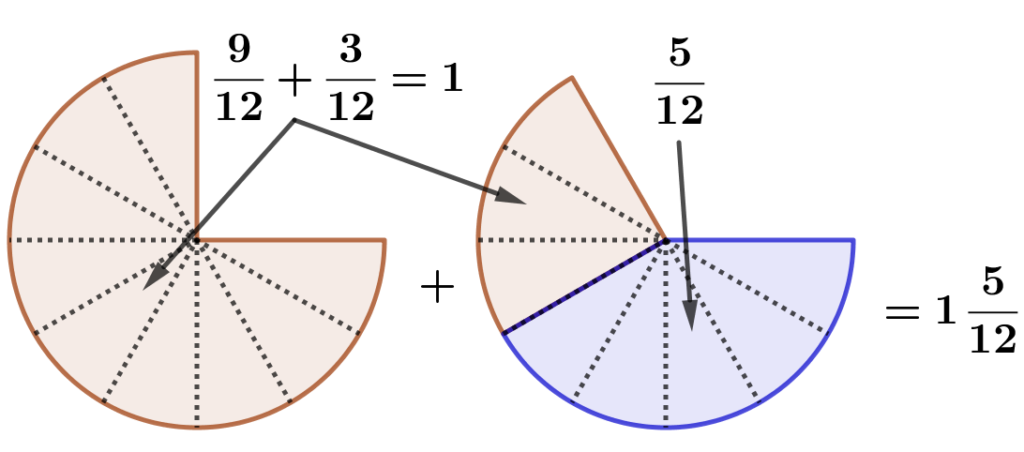Weil nun alle Schnitten die selbe Größe haben, brauchen wir nun nur mehr abzählen, wie viele solche Teile wir insgesamt haben. Es sind 9 + 8 = 17 Schnitten. \frac{3}{4} einer Pizza und \frac{2}{3} einer Pizza ergeben insgesamt \color{brown}\mathbf{\frac{17}{12}} einer Pizza, das ist \textcolor{brown}{\textbf{eine ganze}} Pizza und \color{blue}\mathbf{\frac{5}{12}} einer weiteren Pizza, bzw. \mathbf{\color{brown}1 \color{blue}\frac{5}{12}} Pizzen.
Rechengesetz für die Addition und die Suktraktion von Brüchen
Brüche werden addiert bzw. subtrahiert, indem man die Brüche “gleichnamig” macht, d.h. man bestimmt einen gemeinsamen Nenner und bringt jeden Summanden auf diesen gemeinsamen Nenner. Als gemeinsamen Nenner bestimmt man sinnvollerweise das kleinste gemeinsame Vielfache (kgV) der Nenner der beiden Summanden.
\boxed{\mathbf{\frac{a}{b} \pm \frac{c}{d} = \frac{a \cdot d}{b \cdot d} \pm \frac{c \cdot b}{b \cdot d} = \frac{ad \pm bc}{bd}}}Multiplikation und Division rationaler Zahlen
Multiplikation mit einer natürlichen Zahl
Von einem Mittagessen mit vier Personen ist von jeder Person \frac{1}{3} ihrer Pizza übrig geblieben. Wie viele Pizzen sind insgesam übrig geblieben?
Das Ergebnis erhalten wir aus der Multiplikation \frac{1}{3} \cdot 4. Weil die Multiplikation aber Addition geschrieben werden kann, erhalten wir:
\mathbf{\frac{1}{3} \cdot 4} = \frac{1}{3} + \frac{1}{3} + \frac{1}{3} + \frac{1}{3} = \frac{1 + 1 + 1 + 1}{3} = \frac{1 \cdot 4}{3} = {\frac{4}{3}}Allgemein gilt für die Multiplikation einer rationalen Zahl mit einer natürlichen Zahl:
\boxed{\mathbf{\frac{a}{b} \cdot c = \frac{a\cdot c}{b},\; \; \; a \in \mathbb{Z},\; b, c \in \mathbb{N}\;\;\; b \ne 0}}Eine rationale Zahl \frac{a}{b} wird mit einer natürlichen Zahl c multipliziert, indem man den Zähler mit der natürlichen Zahl c multipliziert.
Division durch eine natürliche Zahl
Wenn ich \frac{3}{4} einer Pizza habe und ich möchte diese in zwei gleich große Teile teilen, dann ist jede Hälfte nur mehr halb so gr0ß. Die Pizza besteht aus 3 Vierteln. Halbiere wir jedes Viertel, werden daraus Achtel. Jede Hälfte besteht dann aus 3 Achteln, d.h. \frac{3}{4} \div 2 = \frac{3}{8}.
Dieses Ergebnis erhält man auch durch Anwendung der Rechenregeln für die Addition und Multiplikation von Zahlen:
\begin{array}{clc}&\mathbf{\frac{3}{4} \div 2} & = \\ =&\left( 3 \div 4 \right)\div 2&= \\ = & 3 \div \left( 4 \cdot 2 \right) & =\\ =& 3 \div 8 &= \\ =& \mathbf{\frac{3}{8}} \end{array}Allgemein gilt für die Division einer rationalen Zahl durch eine natürliche Zahl:
\boxed{\mathbf{\frac{a}{b} \div c = \frac{a}{b \cdot c},\; \; \; a \in \mathbb{Z},\; b, c \in \mathbb{N}\;\;\; b, c \ne 0}}Eine rationale Zahl \frac{a}{b} wird durch eine natürliche Zahl c dividiert, indem man den Nenner mit der natürlichen Zahl c multipliziert.
Multiplikation mit einer rationalen Zahl
Sollen wir das Produkt der beiden rationalen Zahlen \frac{2}{3} und \frac{5}{4} bilden, können wir dies tun, indem wir auf die oben angegebenen Rechengesetze zurückgreifen:
\begin{array}{clc}&\mathbf{\frac{2}{3}\cdot \frac{5}{4}}&= \\ =& \frac{2}{3} \cdot \left( 5 \cdot \frac{1}{4}\right)&= \\ =& \left( \frac{2}{3} \cdot 5\right) \div 4 &= \\ =& \frac{10}{3} \div 4 &= \\ =& \mathbf{\frac{10}{12}} &= \\=& \mathbf {\frac{2 \cdot 5}{3 \cdot 4}}&\end{array}Allgemein gilt für die Multiplikation zweier rationaler Zahlen:
\boxed{\mathbf{\frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d},\; \; \; a, c \in \mathbb{Z},\; b, d \in \mathbb{N}\;\;\; b, d \ne 0}}Eine rationale Zahl \frac{a}{b} wird mit einer rationalen Zahl \frac{c}{d} multipliziert, indem man Zähler mit Zähler und Nenner mit Nenner multipliziert.
Division durch eine rationale Zahl
Wie die Multiplikation zweier rationaler Zahlen kann auch die Division einer rationalen Zahl \frac{a}{b} durch eine rationale Zahl \frac{c}{d} durch die Anwendung der Rechengesetze für die Multiplikation und die Addition mit ganzen Zahlen zurückgreifen:
\begin{array}{clc}&\frac{a}{c} \div \frac{c}{d}&= \\ =& \left( a \div b\right) \div \left( c \div d \right) &=\\ =& a \div \left( b \cdot \left( c \div d \right) \right) &= \\ =& a \div \left( b \cdot c \div d \right)&= \\ =& a \div \left( b \cdot c \right) \cdot d &= \\ =& \left( a \cdot d \right) \div \left( b \cdot c \right)&= \\ =& \frac{a \cdot d}{b \cdot c}&\end{array}.
Zusammenfassend gilt:
\boxed{\mathbf{\frac{a}{b} \cdot \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{a \cdot d}{b \cdot c}\;\;\;a, b \in \mathbb{Z}\;\;c, d \in \mathbb{N}^{+} }}Brüche werden dividiert, indem man den Dividenden mit dem Kehrwert des Divisors multipliziert.
Doppelbrüche:
Mit der Regel für die Division rationaler Zahlen lassen sich auch Doppelbrüche berechnen:
\boxed{\mathbf{\frac{\frac{a}{b}}{\frac{c}{d}} = \frac{a}{b} \div \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{a \cdot d}{b \cdot c}}}