Der Hauptsatz der Satzgruppe des Pythagoras kann verwendet werden, um die Wurzel aus n mit n \in \mathbb{R}, d.h. \sqrt{2}, \sqrt{3}, \sqrt{4}, \sqrt{5}, \sqrt{6}, ... , zu konstruieren. Weil bei der Konstruktion der Haptsatz des Pythagoras verwendet wird, die entstandene Figur als Schnecke das Pythagoras oder Wurzelschnecke bezeichnet.
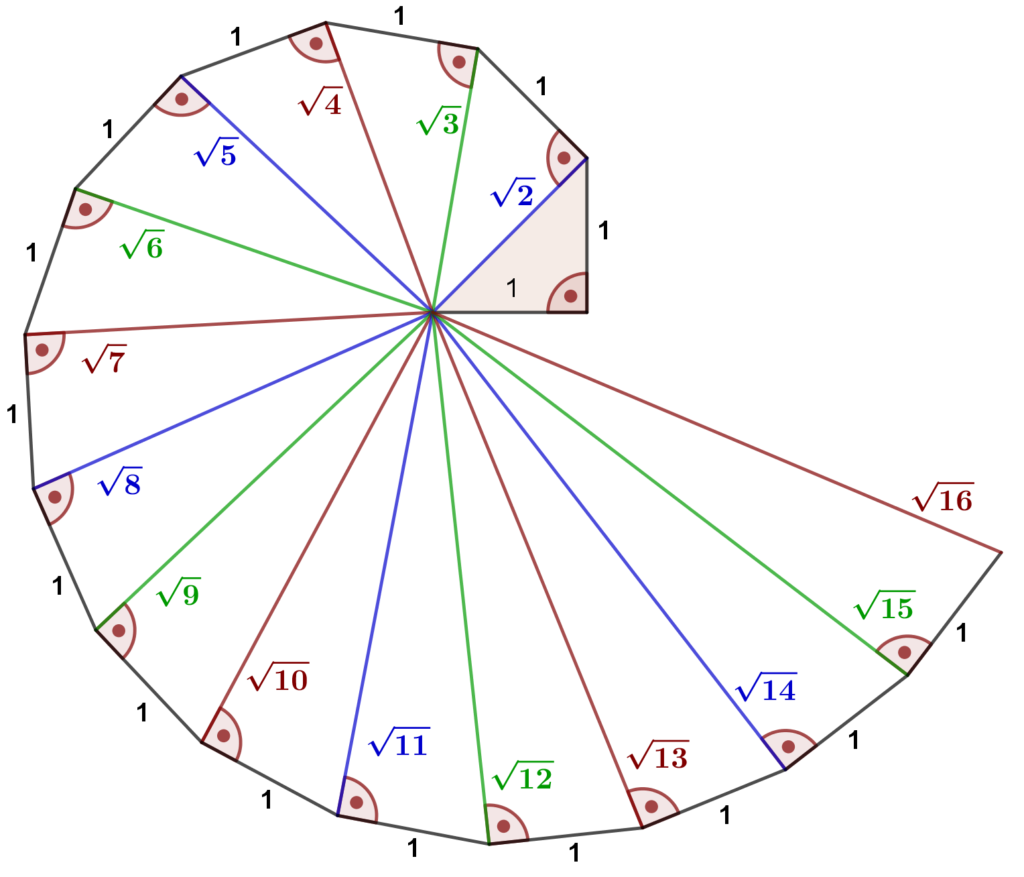Dabei geht man von einem rechtwinkligen Dreieck mit den Kathethenlängen 1 aus. Die Hypotenuse hat dann, wegen des Hauptsatzes die Länge \sqrt{1^2 + 1^2} = \sqrt{2}.
Die so erhaltene Hypotenuse mit der Länge \sqrt{2} nehmen wir nun als Kathetenlänge für das nächste rechtwinkelige Dreieck. Über dieser Kathete zeichnen wir eine weitere Kathete mit der Länge 1. Die nächste Hypotenuse hat dann die Länge \sqrt{\left( \sqrt{2}\right)^2 + 1} = \sqrt{3}.
Diesen Prozess setzen wir beliebig oft fort. Auf diese Weise erhalten wir die in obenstehender Abbildung dargestellte Schnecke des Pythagors.
Betrachten wir von dieser Schnecke eine beliebige Zahl \sqrt{n}, dann ergibt sich die nächste Zahl aus:
\mathbf{\sqrt{\left( \sqrt{n}\right)^2 + 1} = \sqrt{n+1}}Mit diesem Verfahren ließe sich prinzipiell für jede beliebige natürliche Zahl n der Wert \sqrt{n} konstruieren.
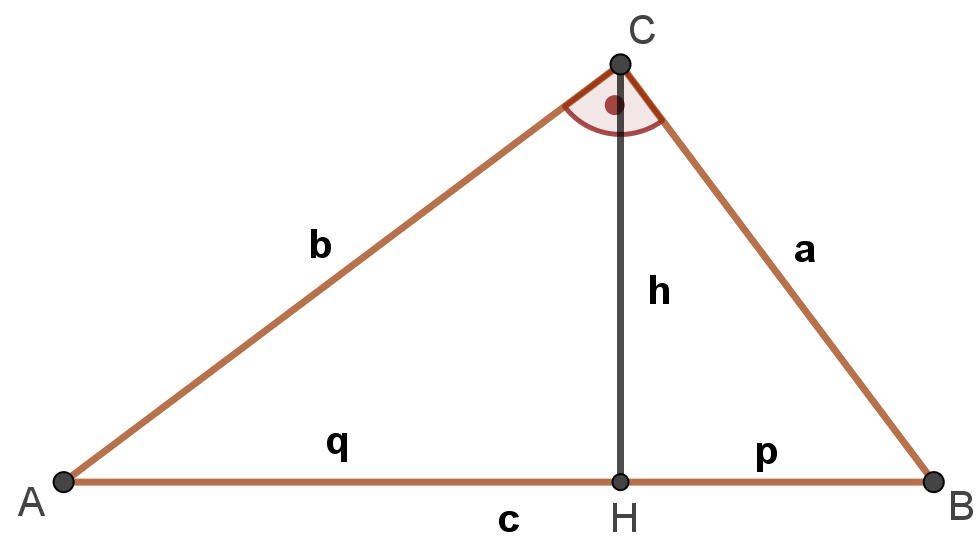
Konstruktion von \sqrt{n} mit Hilfe des Höhensatzes
Wegen des Höhensatzes gilt:
h^2 = q \cdot p~~~~~\Rightarrow~~~h = \sqrt{q \cdot p}
Zerlege die Zahl n in ein Produkt p \cdot q zweier natürlicher Zahlen p und q.- Trage in einem Koordinatensystem auf der x-Achse die Strecke q + p auf.
- Zeichne über der Strecke \overline{qp} den Thaleskreis mit dem Mittelpunkt M.
- Zeichne im Punkt H eine Gerade h normal auf die x-Achse.
- Schneide die Gerade h mit dem Thaleskreis und bezeichne den Schnittpunkt mit C.
- Die Länge der Strecke HC entspricht dem Wert von \sqrt{n}.
Zerlege die Zahl Beispiel: Konstruiere mit Hilfe des Höhensatzes den eine Strecke mit der Länge \sqrt{16}
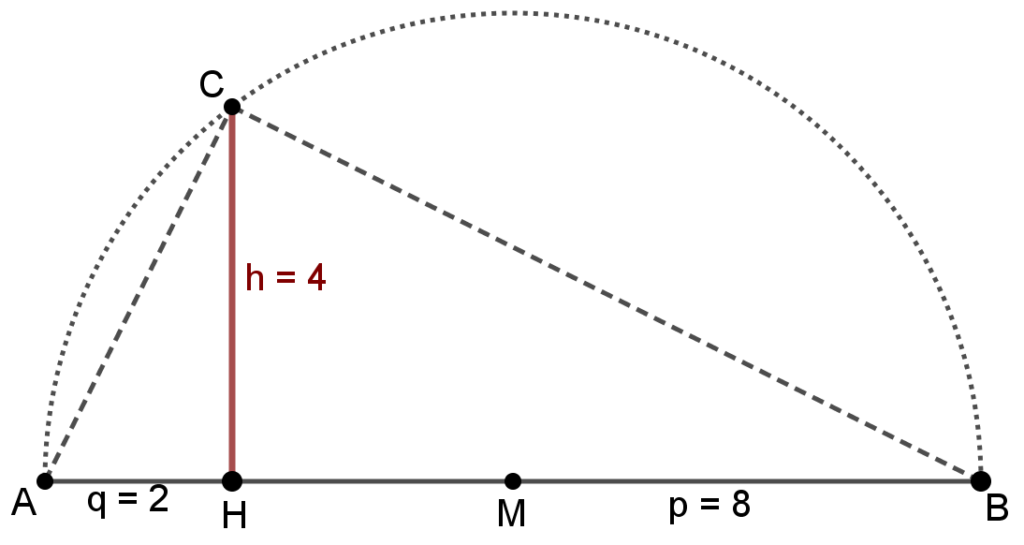Zerlegung der Zahl 16 in ein Produkt zweier natürlicher Zahlen. Eine mögliche Zerlegung ist 16 = 2 \cdot 8~~\Rightarrow~~~q = 2,~p = 8.
Die strecken q und p bilden die Hypotenuse eines rechtwinkeligen Dreiecks, das mit Hilfe eines Thaleskreises konstruiert werden kann. Die Länge der Höhe h in diesem Dreieck ergibt den gesuchten Wert von \sqrt{16}.
Beispiel: Konstruiere mit Hilfe des Höhensatzes den eine Strecke mit der Länge \sqrt{17}
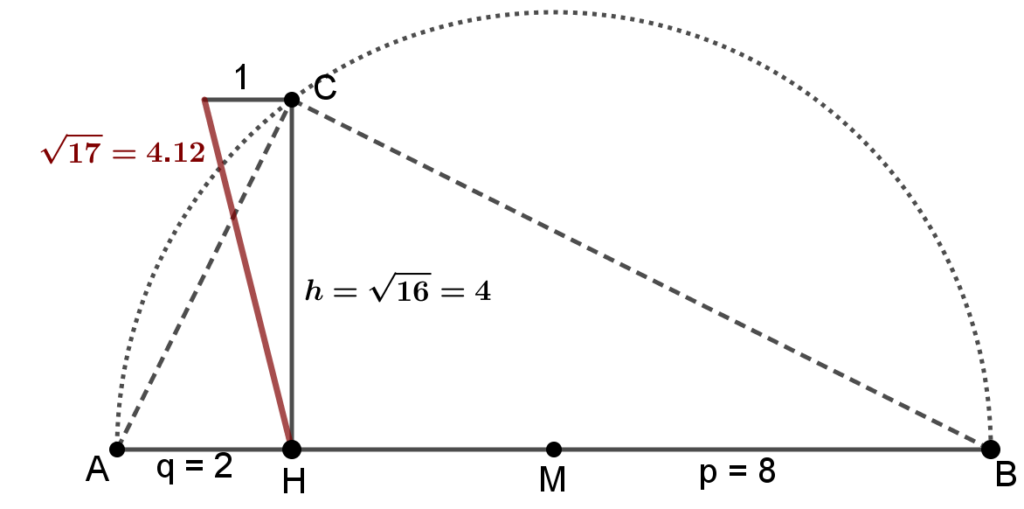Der Ausdruck \sqrt{17} lässt sich wie folgt schreiben:
Die Länge der Strecke \sqrt{16} haben wir in der obige Abbildung bereits konstruiert. Durch Anwendung des Hauptsatzes des Pythagoras kann dann \sqrt{17} wie folgt konstruiert werden:
Konstruktion mit der Differenz von Quadratzahlen
Quadratzahlen sind jene Zahlen, die sich aus der Multiplikation einer natürlichen Zahl mit sich selbst ergeben. Die ersten zehn Quadratzahlena^2 ergeben isch aus den natürlichen Zahlen a = 1,2, ..., 10:
a:~~~~~1~~2~~~3~~~~~4~~~~~5~~~~~6~~~~~7~~~~~8~~~~~9~~~~10 \newline a^2:~~~1~~4~~~9~~~16~~~25~~~36~~~49~~~64~~~81~~~100Die Differenz zweier aufeinanderfolgender Quadratzahlen ergibt:
a^2:~~~~~~~1~~~4~~~9~~~16~~~25~~~36~~~49~~~64~~~81~~~100\newlineDifferenz: ~3~~~~5~~~7~~~~~9~~~~11~~~13~~~15~~~17~~~19
Bildet man fortlaufend die Differenz zweier aufeinanderfolgender Quadratzahlen erhält, man die ungeraden natürlichen Zahlen. Im Umkehrschluss kann man sagen, dass sich jede ungerade Zahl als Differenz zweier benachbarter Quadratzahlen schreiben lässt.
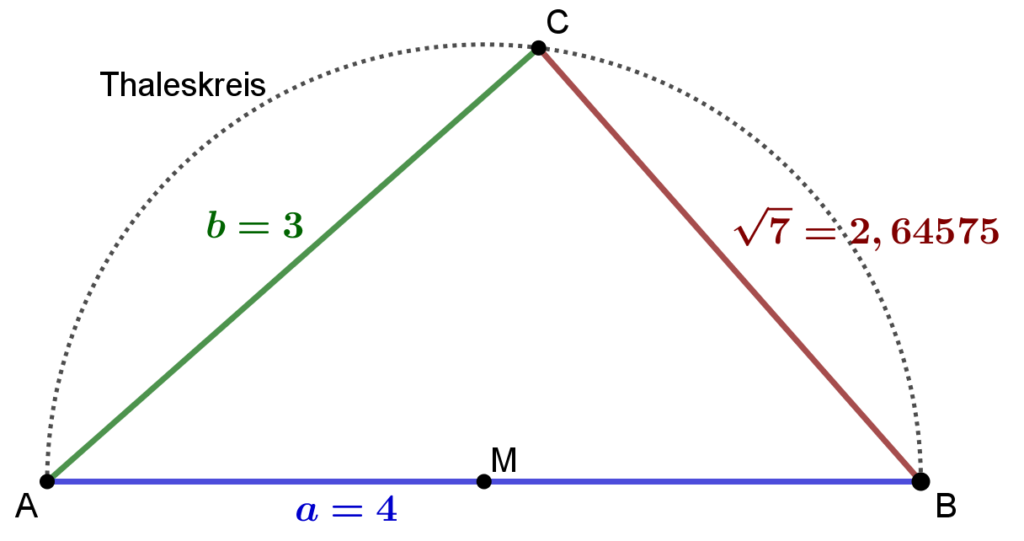Beispiel: 7 = 16 - 9 = 4^2 - 3^2 = \left( \sqrt{7}\right)^2
Allgemein kann dieser Zusammenhang für zwei benachbarte Quadratzahlen a und b,~a>b geschrieben werden als:
a^2 - b^2 = \left( \sqrt{n}\right)^2 \newlineDie Wurzel \sqrt{n} lässt sich dann mit Hilfe des Hauptsatzes des Pythagoras wie folgt konstruieren:
- Zeichne auf der x-Achse eine Strecke AB mit der Länge der größeren der beiden Quadratzahlen (also a).
- Zeichne über dieser Strecke den Thaleskreis.
- Schlage vom Punkt A aus die Länge der zweiten Quadratzahl (also b) ab.
- Die Länge der zweiten Kathete entspricht dann dem Wert von \sqrt{n}.